27: Problem 27.50

INTRO:(Figure 1) shows two very large slabs of metal that are parallel and distance l apart. The top and bottom surface of each slab has surface area A. The thickness of each slab is so small in comparison to its lateral dimensions that the surface area around the sides is negligible. Metal 1 has total charge Q₁=Q and metal 2 has total charge Q₂=2Q. Assume Q is positive.

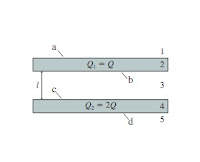
Figure 1

-----------------------------------------------------------------------------------------------------
PART A:
Determine the electric field strength E₁ in region 1. Give your answer as a multiple of Q/ε₀.
Express your answer in terms of some or all of the variables l, A, Q, and the constant π.

SOLUTION:
One Gaussian surface is a cylinder with end-area a extending past the two metal slabs. A second Gaussian surface ends in region 3, the space between the slabs

Using Gauss's Law, ∫E⋅dA = ∫_top E⋅dA + ∫_bottom E⋅dA + ∫_sides E⋅dA = E₁a + E₅a + 0 = Q_in / ε₀

The total charge per unit area on both surfaces of the top slab is Q₁/A = Q/A, so the charge enclosed within the cylinder is Qa/A.

Similarly, the enclosed charge on the lower slab is Q₂a/A = 2Qa/A

Thus, E₁a + E₅a = Qa/(A⋅ε₀) + 2Qa/(A⋅ε₀) = 3Qa/(A⋅ε₀)
∴ E₁ + E₅ = 3Q/(A⋅ε₀)

Fields E₁ & E₅ are both a superposition of the fields of four sheets of surface charge. Because the field of a plane of charge is independent of distance from the plane, the superposition at points above the top plane must be the same magnitude, but opposite direction, as the superposition at points below the bottom plane. 

∴ E₁ = E₅ = 1/2(3Q/(A⋅ε₀))

E₁ = 3/2A ⋅Q/ε₀

-----------------------------------------------------------------------------------------------------
PART B:
Determine the electric field strength E₂ in region 2. Give your answer as a multiple of Q/ε_0.
Express your answer in terms of some or all of the variables l, A, Q, and the constant π.

SOLUTION:
Because these are metals we immediately know that E₂ = E₄ = 0
0

-----------------------------------------------------------------------------------------------------

PART C:

Determine the electric field strength E₃ in region 3. Give your answer as a multiple of Q/ε₀.
Express your answer in terms of some or all of the variables l, A, Q, and the constant π.

SOLUTION:

Consider the Gaussian surface on the right. The lower slab is more positive than the upper slab, so the electric field in region 3 must point upward, into the lower face of this cylinder.

∫E⋅dA = ∫_top E⋅dA + ∫_bottom E⋅dA + ∫_sides E⋅dA = E₁a - E₃a + 0 = Q_in / ε₀

where the minus sign with E₃ is because of the direction.  We know E₁, and we've already determined Q_in = Qa/A.

Thus, E₃ = E₁ - Q/(A⋅ε₀) = 3Q/(2A⋅ε₀) - Q/(A⋅ε₀) 

∴ E₃ = Q/(2A⋅ε₀)

E₃ = 1/2A ⋅Q/ε₀

-----------------------------------------------------------------------------------------------------

PART D:

Determine the electric field strength E₄ in region 4. Give your answer as a multiple of Q/ε₀.

Express your answer in terms of some or all of the variables l, A, Q, and the constant π.

SOLUTION:

See part B

0

-----------------------------------------------------------------------------------------------------

PART E:

Determine the electric field strength E₅ in region 5. Give your answer as a multiple of Q/ε₀.

Express your answer in terms of some or all of the variables l, A, Q, and the constant π.

SOLUTION:

See Part A

E₅ = 3/2A ⋅Q/ε₀

-----------------------------------------------------------------------------------------------------

PART F:

Determine the surface charge density η_a on the surface a. Give your answer as a multiple of Q/A.

SOLUTION:

The electric field at the surface of a conductor is E = η/ε₀

We can use the known fields and η = ε₀E to find the four surface charge densities.  

At surface a, E₁ points away from the surface, Thus

η_a =  ε₀E₁ = ε₀⋅3Q/(2A⋅ε₀) = 3Q/(2A)

η_a = 3/2⋅Q/A

-----------------------------------------------------------------------------------------------------

PART G:

Determine the surface charge density η_b on the surface b. Give your answer as a multiple of Q/A.

SOLUTION:

At surface b, E₃ points toward the surface, Thus

η_b =  -ε₀E₁ = -ε₀⋅Q/(2A⋅ε₀) = -Q/(2A)

η_b = -1/2⋅Q/A

-----------------------------------------------------------------------------------------------------

PART H:

Determine the surface charge density η_c on the surface c. Give your answer as a multiple of Q/A.

SOLUTION:

Surface c is opposite to surface b, because the field points away from the surface.
Therefore, η_c = - η_b = Q/(2A)

η_c = 1/2⋅Q/A

-----------------------------------------------------------------------------------------------------

PART I:

Determine the surface charge density η_d on the surface d. Give your answer as a multiple of Q/A.

SOLUTION:

At surface d, the field points away from the surface and has the same strength as E₁
Therefore, η_d = η_a = 3Q/(2A)

η_d = 3/2⋅Q/A

-----------------------------------------------------------------------------------------------------